On mesure parfois les inégalités de revenus ou de patrimoine dans une population donnée à l’aide du coefficient de Gini. Rien à voir avec la boisson des années 1980. À base de quinine. D’ailleurs je n’ai jamais compris pourquoi c’était précisé « à base de quinine ». Comme si c’était un plus marketing. À la limite, ça paraît un peu louche, un peu étrange. Un dérivé de quinoa, sans doute issu de délires industriels. Comme la lécithine de soja. Est-ce que ma grand-mère utilise du glutamate de sodium ? Bref.

Le coefficient de Gini – rien à voir non plus avec les frères Karamazov – est juste une mesure. Je ne suis pas bien certain de quoi. Mais c’est comme la température corporelle, ou la pression artérielle : du moment que nous réussissons à couvrir nos angoisses existentielles sous des couches de névroses retenues, on ne s’en soucie guère.

Et alors voilà. Imaginez. Vous rangez tout le monde par ordre croissant de revenus. Les démunis à gauche, les milliardaires à droite. Et pourquoi « démunis » ? Naissons-nous munis ? Parlons des nus, donc. Puisque c’est bien là tout ce que nous avons au début. Nous nus. Je ne parle pas des naturistes, nudistes, numismates et autres numérologues, qui ont peu ou prou eu le choix de leur nullité. Nous nés nus. Phares. Mais je m’égare. D’Austerlitz. De courses. De cheval. De course.

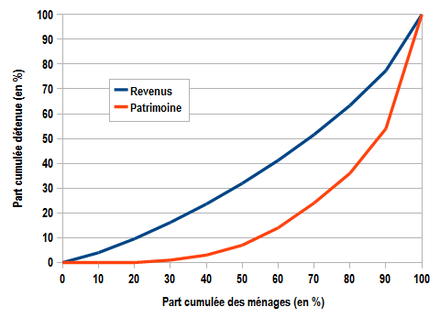
En cumulant leurs revenus respectifs, nous constatons une courbe qui démarre plutôt plate et dont la pente s’accentue au fur et à mesure.

Imaginons un cas extrême où la courbe est totalement plate, au niveau zéro, jusqu’au dernier individu, qui est le seul à gagner la totalité des revenus de la population. C’est le cas d’une famille dont un seul des membres touche des revenus. C’est une répartition absolument inégale. Dans ce cas, le coefficient vaut 1.

À l’opposé, si tout le monde gagne la même chose, le cumul des revenus est régulier, uniforme. Une belle progression linéaire. L’égalité est parfaite, au sens mathématique. Et sans doute aussi d’une certaine manière au sens d’une forme d’idéal communiste – je ne sais jamais s’il faut dire collectiviste, socialiste, marxiste, utopiste, d’atterrissage. Car je suis en vol entre Barcelone et Paris, ne me demandez pas pourquoi ; d’un point de vue purement géologique cela n’aurait aucun sens. Et dans ce cas le coefficient vaut 0.

Notons que l’axologie proposée par ce coefficient suggère que l’égalité parfaite est nulle. Ce n’est qu’une suggestion, une opinion. Et les opinions, ça fait pleurer mais c’est tellement bon à la poêle. À moins que ce ne soit les oignons.

Au niveau mondial, le coefficient de Gini a connu un pic dans les années 1920. L’essor des pays dits aujourd’hui industrialisés, au détriment des détenteurs de ressources naturelles, a favorisé l’enrichissement rapide d’une catégorie de la population plus vive et cupide que la moyenne. Ce n’est qu’une hypothèse que je pose. Oui, je sais, je mets des affaires partout. Et parfois, même, je ne les retrouve pas quand j’en ai besoin. Et alors je m’en veux d’être aussi bordélique. Quoique je n’aie jamais fréquenté de bordel. Il est donc incorrect que j’emploie ce terme. Certaines maisons closes étaient d’ailleurs réputées être très bien tenues. Nous mettons là le doigt sur un sujet épinemment polémique – hybride barbare entre une épine et une éminence, qui n’est pas qu’une marque de survêtements surannés.

Le coefficient de Gini s’est ensuite rapidement réduit et stabilisé pendant les « Trente Glorieuses ». Pour reprendre une hausse rapide entre 1980 et 2010. Avant de commencer à diminuer à nouveau. Ce qui tendrait à montrer que les pauvres sont en moyenne au niveau mondial de moins en moins pauvres, à quelques hypothèses simplificatrices mais sensées près.

On ne peut rien en conclure au niveau local d’un pays, d’une région, et, a fortiori, d’un individu. Et je ne mets pas d’accent sur le « a » de « a fortiori » parce que je suis pédant, voire bipédant quand il m’arrive de ne pas me déplacer à cloche-pied. Où l’on ne comprend pas ce que les cloches ont à voir là-dedans.

Dans ma famille, par exemple, les revenus de mes enfants restent parfaitement nuls, et ce depuis de nombreuses années.

Nous retiendrons finalement que, malgré toutes ces bougies parfumées et ces canapés en kit, la Scandinavie présente les coefficients de Gini les plus faibles du monde.

Hej.

J’ai lu un livre sur π.

Ce qu’il faut en retenir, dans les grandes lignes:

• π, prononcé «pi», est une valeur constante. C’est le nombre de diamètres qu’il y a dans la circonférence d’un même cercle. C’est assez vertigineux de se dire qu’il y a des choses qui ne changent pas dans ce bas monde. Voire qui existeront encore après la fin de notre univers.
  
• 3,14 en est une très bonne approximation. Par exemple, prenons une planète de 12 750 km de diamètre. L’erreur d’approximation du calcul de sa circonférence est d’environ 20 km – soit moins d’une heure de course à pied pour n’importe quel kényan. Plus généralement, selon Isaac Asimov, si l’univers était une sphère de diamètre 80 000 millions d’années-lumière, l’erreur commise avec 35 décimales de π serait inférieure à un millionième de centimètre.
• On ne peut pas « construire » π avec une règle et un compas. Ni avec une bite et un couteau. Quoi que. π est en effet un nombre transcendant. Non pas qu’il soit véritablement au-dessus du lot, mais, en mathématiques, cela signifie qu’il ne peut pas être la solution d’une équation classique, vous savez, genre ax²+bx+c=0, grosso modo. Et ça, c’est justement un critère pour être constructible à la règle et au compas. L’homme de Vitruve – vous savez, le dessin de Léonard de Vinci, avec les jambes qui raccourcissent quand elles s’écartent – n’en était pas à cette approximation près. La quadrature du cercle n’est pas possible.
• Il y a encore des mathématiciens qui travaillent sur des formules pour calculer le plus rapidement possible le plus grand nombre de décimales de π possible. C’est beau. Cela me rappelle une phrase de Jacqueline de Romilly – en substance parce que j’ai oublié d’où ça vient : « Tant qu’il y aura une petite fille qui travaille son violon le soir dans sa chambre, la civilisation ne sera pas perdue. »